The Sound of Music

Oscilloscopes and guitars are a wonderful combination :-)

This is what an open-E played on the 6th string of my Stratocaster knock-off looks like:-



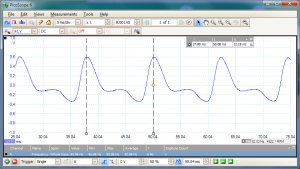
The two vertical dashed lines measure that time between two consecutive peaks (12.19ms) and from this we can work out that the fundamental frequency is 82Hz (as it should be...E on the 6th string is supposed to be 82.4Hz).

The scope can also do spectrum analysis (showing the harmonic content).  Here's the same open-6th string:-



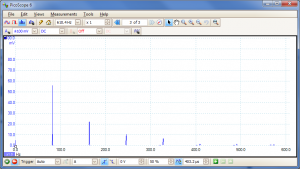
Unsurprisingly, you see a strong peak at 82.4Hz (the fundamental) with 1st harmonic (164Hz, one octave above), 2nd (247Hz, which is B on the 2nd string, nicely illustrating the relationship to the 5th note in a chord) and 3rd (329Hz, which is the E on the 1st string, two octaves above the fundamental) all strongly present.  Although there isn't much of it, 4th harmonic occurs at 412Hz (you can just barely see it).  This is G# played on the 1st string which illustrates the role of the major 3rd note in a chord.  I think its interesting to see how the notes of a major chord all occur as harmonics of the fundamental.

Another interesting thing to look at is how tuning using harmonics works.  This is the 6th string with me barely touching the string just above the 12th fret to damp the first harmonic:-



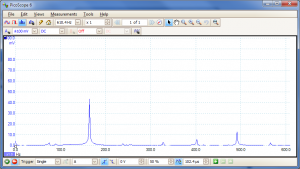
Two interesting things:  the strongest peak is at 164Hz (one octave above that open E, just as you would expect).  The fundamental frequency of that string is almost completely gone (because my finger prevents the string from moving at its centre point).  Also, there is very little other harmonic content.  Sure enough, if I graph the signal it is much closer to being a pure sine wave at 164Hz:-



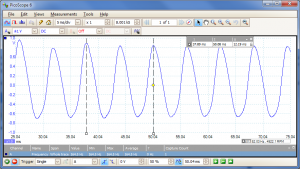
If you play that with another (nearly) pure sine wave which is only slightly different (i.e. fractionally out of tune) they will interfere with each other, creating that "fading in and out" effect that we listen for when tuning using harmonics.  They will fade in and out at a rate equal to the frequency difference (which is why you can only hear it when you are very close...tuned to within a few Hz)

These graphs illustrate this pretty well.  Here are harmonics on two strings (6th string 5th fret and 5th string 7th fret) which are slightly out of tune:-



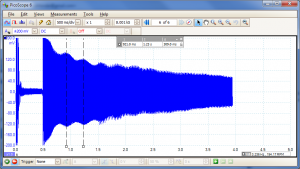
The "waviness" in the signal shows the interference between the two (at ~3Hz, measured with the vertical dashed lines) which I can hear as the characteristic fading in and out.  When I correct the tuning and repeat the test...



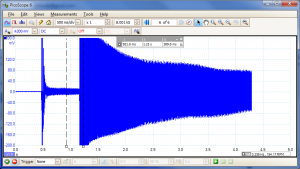
...the "waviness" is gone.  This video illustrates what is going on:-

 

Finally, it is interesting to see the harmonic content of the same note played on two different strings.  Here's the open 5th:-



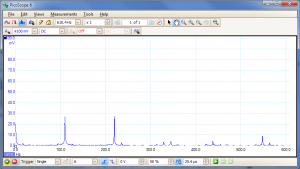
And here's the same A played on the 5th fret of the 6th string:-



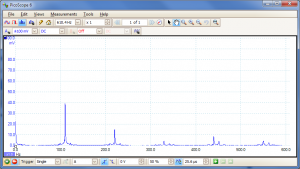
Note the much stronger fundamental (110Hz) compared to the 1st harmonic.